


Codes pour la stéréophotométrie
Sur cette page sont fournis quelques codes Matlab utiles à la résolution du problème de stéréophotométrie. Tous ces codes ont été développés au sein de l'équipe VORTEX à l'IRIT, UMR CNRS 5505 de l'Université de Toulouse in Toulouse, France.
Chaque code inclut une référence vers la publication associée.
Questions / Suggestions : yvain \dot queau \at enseeiht \dot fr (page perso)
Liste des codes
- Stéréophotométrie colorée
- Reconstruction 3D à partir d'un champ de gradient dense
- Fusion variationnnelle d'une carte de profondeur avec une estimation haute précision du gradient de la surface
- Jeux de données
- Edge-Preserving Integration on Arbitrary Domain
- Intégration aux moindres carrés pondérés sur un domaine quelconque
- Intégration aux moindres carrés sur un domaine rectangulaire
- Stéréophotométrie non calibrée
Stéréophotométrie colorée
Éclairages directionnels
Ces scripts montrent comment résoundre la stéréophotométrie avec des données RGB, par une approche variationnelle résolvant un système d'EDPs linéaires obtenues par les ratios d'images. L'archive contient :
- Deux jeux de données : l'un est lambertien (billet de 10 euros) et l'autre présente de forts effets de réflexions mutuelles (pièce de 50 centimes). Les directions d'éclairages sont fournies.
- Une fonction d'estimation de la profondeur par stéréophotométrie fondée sur un système d'EDPs linéaires.
- Deux scripts de démonstration.






Source Code
Fichiers .m : ici.
Références
Unbiased Photometric Stereo for Colored Surfaces: a Variational ApproachQuéau, Y. and Mecca, R. and Durou, J.-D.
Computer Vision and Pattern Recognition (CVPR 2016)
Paper (pdf)
Éclairages ponctuels
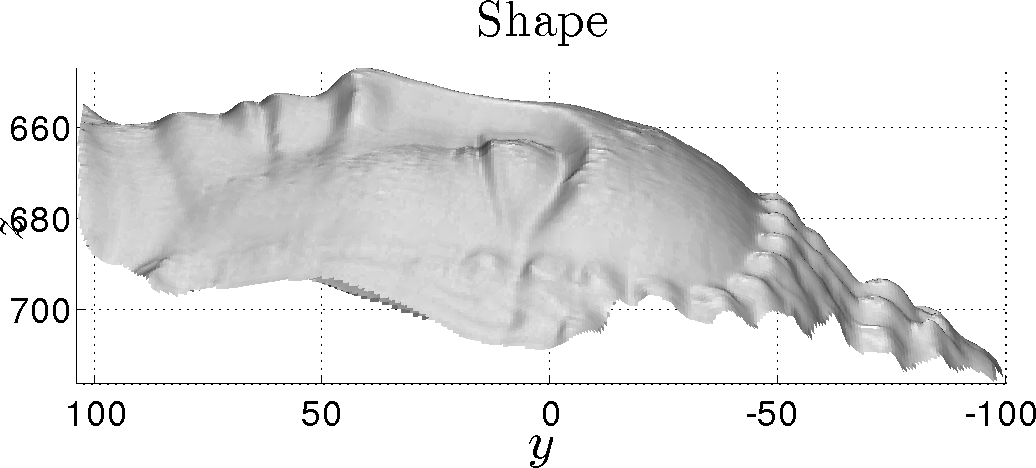
Résolution de la stéréophotométrie couleur sous des éclairages ponctuels. La non-linéairité dûe à l'éclairage est éliminée grâce à un schéma de point fixe. L'archive contient:
- Un jeu de données : 8 images d'un buste en plâtre sous des éclairages proches induits par des LEDs calibrées (intensités et positions).
- Une fonction pour l'estimation de la profondeur en moindres carrés, par un algorithme de point fixe.
- Un script de démonstration.


Source Code
Fichiers ".m" : ici.
References
Unbiased Photometric Stereo for Colored Surfaces: a Variational ApproachQuéau, Y. and Mecca, R. and Durou, J.-D.
Computer Vision and Pattern Recognition (CVPR 2016)
Paper (pdf)
Intégration d'un champ de gradient
Fusion variationnnelle d'une carte de profondeur avec une estimation haute précision du gradient de la surface
Ces scripts montrent comment très simplement fusionner une carte de profondeur (dense ou éparse) avec une estimation précise du gradient de la profondeur (normales), obtenue par exemple par stéréophotométrie. L'archive contient :
- Un scipt pour estimer les normales à la surface par stéréophotométrie
- Un code d'intégration en moindres carrés sur domaines non rectangulaires
- Un code d'intégration prenant en compte des points de contrôle
- Un code d'intégration prenant en compte un a priori dense sur la surface





Source Code
Fichiers .m : ici.
References
Edge-Preserving Integration of a Normal Field: Weighted Least-squares, TV and L1 ApproachesQuéau, Y. and Durou, J.-D.
Scale-Space and Variational Method in computer vision (SSVM 2015)
Paper (pdf)
Reconstruction tridimensionnelle par stéréophotométrie
Quéau, Y.
Thèse de doctorat - chapitre 2
Thèse (pdf)
Jeux de données
Quelques jeux de données, au format Matlab (.mat), qui peuvent être utilisés pour tester les algorithmes de shape-from-gradient, i.e. reconstruire une carte de profondeur à partir d'un champ de gradient dense, obtenu par exemple par stéréophotométrie.
Les jeux de données réels incluent les images de stéréophotométrie , un masque et une estimation du gradient de profondeur. Les jeux de données synthétiques incluent la vérité terrain sur la profondeur et son gradient.
- Buddha dataset (réel, 10 images)
- Synthetic Vase dataset (synthétique, 320x320)
- Canadian Tent dataset (synthétique) : 256x256, 512x512, 1024x1024
Intégration rouste aux discontinuités sur domaine quelconque
Il s'agit des codes correspondant aux trois fonctionnelles discrètes présentées dans notre article SSVM 2015
- Les moindres carrés pondérés (WLS) peuvent être utilisés lorsqu'il est facile de détecter les discontinuités par l'intégrabilité
- La variation totale (TV) isotrope peut être minimisée par moindres carrés repondérés
- la TV anisotrope (norme L1) peut être minimisée par split-Bregman
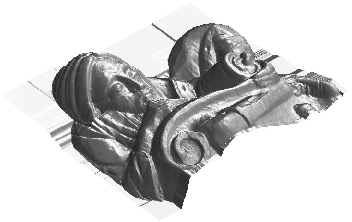
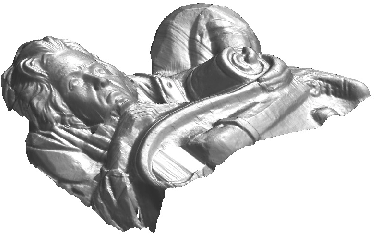
- Ces méthodes itératives peuvent être utilisées pour des problèmes d'édition de surface
Demo des itérations de split-Bregman (L1)

Source Code
Les fichiers ".m", avec un jeu de données, peuvent être téléchargées ici.
Chaque méthode peut être téléchargée séparément :
Reference
Edge-Preserving Integration of a Normal Field: Weighted Least-squares, TV and L1 ApproachesQuéau, Y. and Durou, J.-D.
Scale-Space and Variational Method in computer vision (SSVM 2015)
Paper (pdf)
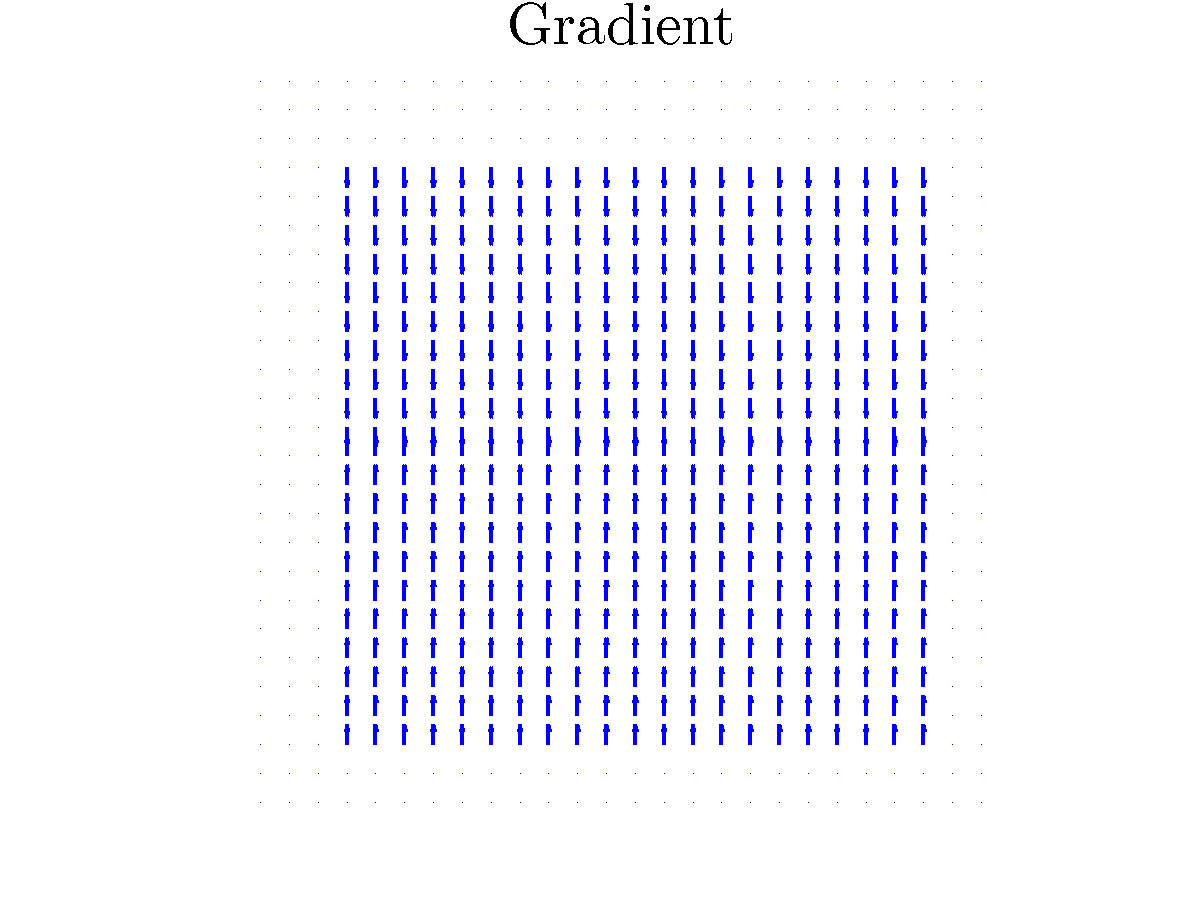
Intégration aux moindres carrés pondérés, sur des domaines connexes quelconques, en utilisant la condition naturelle au bord
Implémentation sur un domaine quelconque en utilisant la factorisation de Cholesky creuse. De plus, le problème aux moindres carrés peut être judicieusement pondéré, de façon à retrouver les discontinuités de profondeur qui sont habituellement lissées (voir les exemples dans l'archive). Cette méthode inclut comme cas particulier la reconstruction aux moindres carrés sur un domaine quelconque.



Code source
Les fichiers ".m", accompagnés d'un script de démo et de deux jeux de données, sont disponibles ici.
Référence
Intégration d'un champ de gradient rapide et robuste aux discontinuités - Application à la stéréophotométrieQuéau, Y. and Durou, J.-D.
Reconnaissance de Formes et Intelligence Artificielle (RFIA 2014)
Intégration rapide sur domaine rectangulaire
Résoudre le problème d'intégration au sens des moindres carrés est équivalent à résoudre une équation de Poisson. Lorsque le domaine d'intégration est rectangulaire, des méthodes de résolution efficaces fondées sur l'algorithme FFT peuvent être utilisées. Suivant la condition aux bords désirée, différentes implémentations peuvent être considérées :
Code source
- Condition aux bords naturelle : Une implémentation de
la méthode de Simchony et al. est proposée ici.
La condition naturelle est celle fournie par le calcul des variations,
et devrrait fournir des résultats plus précis que la condition de Neumann
homogène.
- Condition de Dirichlet : Une implémentation de la méthode de Simchony et al. est proposée ici
- Condition périodique : Une implémentation de la méthode de Frankot et Chellappa est disponible sur la page de Peter Kovesi. Cette méthode est légèrement plus rapide que les précédentes, mais en général la condition périodique n'est pas utilisable.
- Condition de Neumann homogène : an sur la page de Amit Agrawal.
Références
- A method for enforcing integrability in shape from shading algorithms
Frankot, R.T. and Chellappa, R.
IEEE T-PAMI (1988) - Direct analytical methods for solving Poisson equations in computer vision problems
Simchony, T. and Chellappa, R. and Shao, M.
IEEE T-PAMI (1990)
Stéréophotométrie non calibrée
Résolution de l'ambiguïté de bas-relief par la variation totale
Résolution de l'ambiguïté de bas-relief par la régularisation TV du champ M ou de la profondeur.
Etant données trois images ou plus d'un objet acquises sous trois éclairages différents, ce code estime la profondeur, les normales et l'albédo en chaque point.




Code source
Sources Matlab disponibles ici.
Références
- Solving Uncalibrated Photometric Stereo using Total Variation
Yvain Quéau, François Lauze, Jean-Denis Durou
Journal of Mathematical Imaging and Vision (JMIV 2014 - Accepted)
pdf - Solving the Uncalibrated Photometric Stereo problem using Total Variation
Yvain Quéau, François Lauze, Jean-Denis Durou
Fourth International Conference on Scale Space and Variational Methods in Computer Vision (SSVM 2013)
pdf