About

This is the homepage of ELSD (Ellipse and Line Segment Detector). ELSD is a parameterless detector, that can be applied on any grey-scale image without prior edge detection or parameter tuning.

Example:

Original image	ELSD result

The preprint of the article published at ECCV2012 A parameterless line segment and elliptical arc detector with enhanced ellipse fitting. The source code of ELSD can be found here. Note that a newer improved version of the algorithm is available here.
It might be useful to test online our detector, before downloading and compiling it. A demo where users can upload their images and test ELSD is available here demo (user: demo, pass: demo).
Check out the result of ELSD applied on a real video (frame size: 638x360, average execution time 0.7s/frame).
For any questions or remarks, please contact the corresponding author at vpatrauc at gmail dot com.

Abstract

Geometric shape detection (line segment, ellipse) is often a prerequisite for high level tasks; hence we need automatic detectors, i.e. no parameter tuning.

ELSD

• parameterless Ellipse and Line Segment Detector;
• works with grey-scale images (no edge detector needed);
• grounded on the a contrario theory [1], it controls statistically the number of false positives; extends LSD [2];
• it offers a better precision due to enhanced ellipse fitting.

ELSD Overview

We pose the geometric shape detection in the statistical framework of multiple hypothesis testing, in order to focus on reducing/controling false detections.
The main steps of ELSD are:

1. Hypothesis selection:

- heuristic, but free of critical parameters in order to avoid false negatives.

2. Validation:

- parameterless, grounded on a contrario theory; controls the number of false positives.

3. Model selection:

- parameterless; follows Ockham’s razor principle.

1. Hypothesis Selection

This step must produce line segment and elliptical candidates.

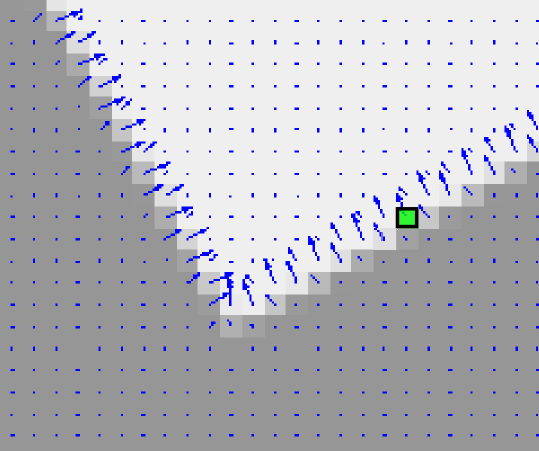
A. Region grow

- starting from a seed pixel, gather recursively neighbour pixels with similar gradient orientation.

B. Curve grow

- gather recursively neighbour regions that follow a convex, roughly smooth contour.

               

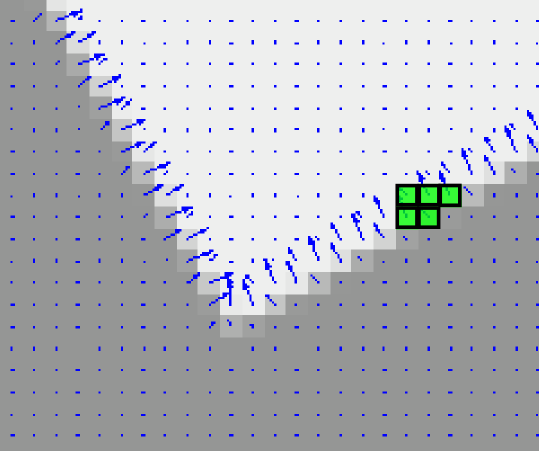
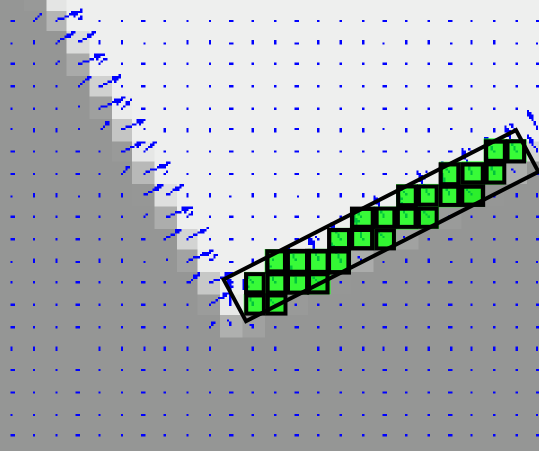
C. Fitting:

- pixels gathered in steps A and B respectively, are used to estimate the line segment and the elliptical hypotheses

• region => rectangle fit => line segment hypothesis;
• curve => circular/elliptical ring fit => circle/ellipse hypothesis.

               

- The tangent to the conic in a point p_i is also the polar of the point p_i w.r.t. the conic [4].
- The algebraic distance error and the gradient orientation error can be simultaneously minimised through a non-iterative procedure. This improves the accuracy, especially when pixels are sampled along incomplete circles/ellipses.

2. A Contrario Validation

The a contrario theory uses the non-accidentalness principle; informally, it says that "we see nothing in noise". Thus, hypotheses that are likely to be observed in noise should be automatically discarded. To this end we need to define two elements: a model of "noise" (unstructured data) and a function to measure the quality (degree of structuredness) of a hypothesis.

Model of unstructured data:

- field of gradients whose orientations can be considered i.i.d. random variables => Gaussian white noise image;

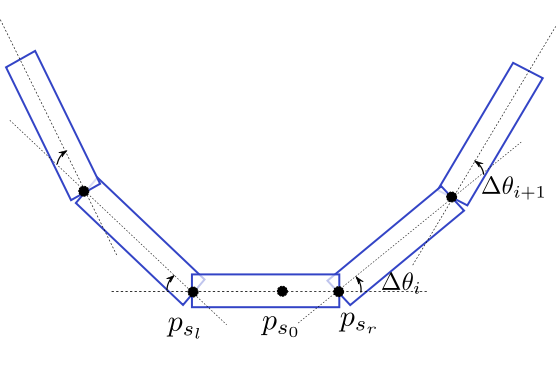
Degree of structuredness:

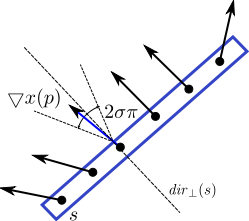
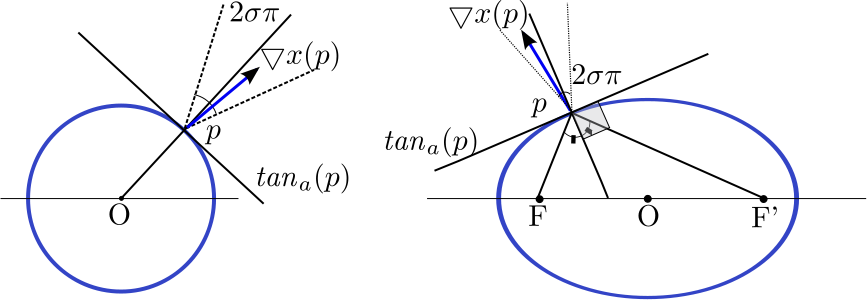
- the number of σ-aligned pixels contained in a hypothesis. For a line segment, a pixel is said to be σ-aligned if its gradient orientation is orthogonal to the line segment, up to a precision σ (see left figure below). Similarly, for circle/ellipse case, a pixel is σ-aligned if its gradient orientation is orthogonal to the tangent to the circle/ellipse in that point (see middle and right figures bellow).

Validation test:

- accept as meaningful hypotheses only those too structured to appear by chance in unstructured data. If a hypothesis contains too many aligned points, it is not likely for it to be observed in noise; thus it is meaningful.

The Number of False Alarms (NFA) is the essential quantity used to assess the validity of a hypothesis, and is given by:
NFA=N⋅Β(l,k,σ), where
N - number of hypotheses (n⁵ line segments, n⁶ circular arcs, n⁸ elliptical arcs, for an nxn image);
l - number of pixels in hypothesis;
k - number of aligned pixels in hypothesis;
Β(l,k,σ) - binomial tail = ∑ ^l_i=k C ^l_i σ ⁱ(1-σ) ^l-i.

A hypothesis is considered meaningful iif it satisfies the validation test NFA ≤ ε.

Control of false positives: If a hypothesis is accepted as meaningful only when the above validation test stands, then the number of meaningful hypotheses observed by chance in unstructured data is less than ε (see the paper for a proof of this proposition).

3. Model Selection

When more than one hypothesis passes the validation test, a model selection needs to be performed to choose the most suitable geometric interpretation for the given data.
Ockham's razor principle recommends to

• choose the best geometric interpretation for the data,
• but penalize complexity.

We use NFA as model selection criterion [3] and keep as valid hypothesis the one with the lowest NFA.

Results

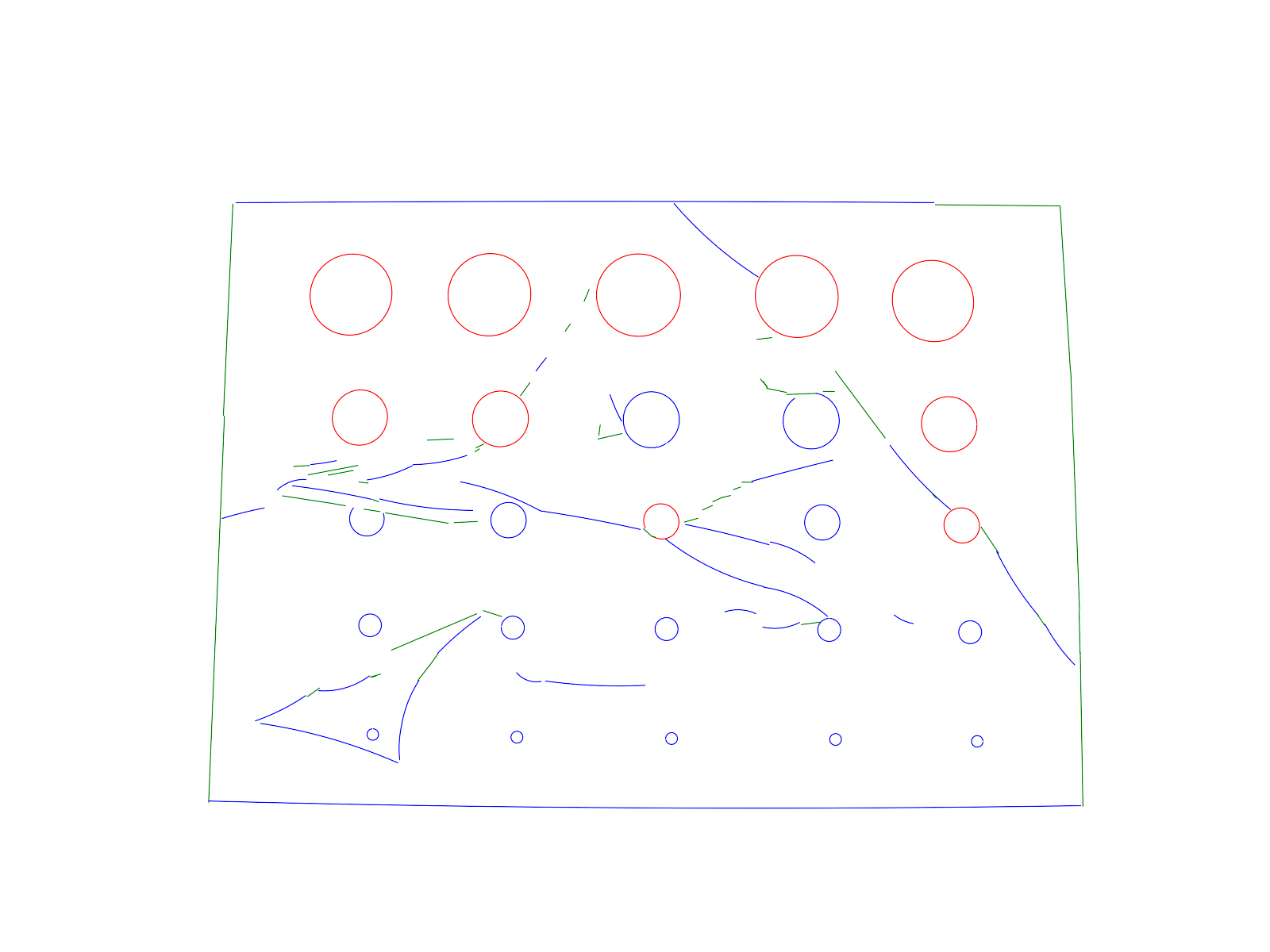
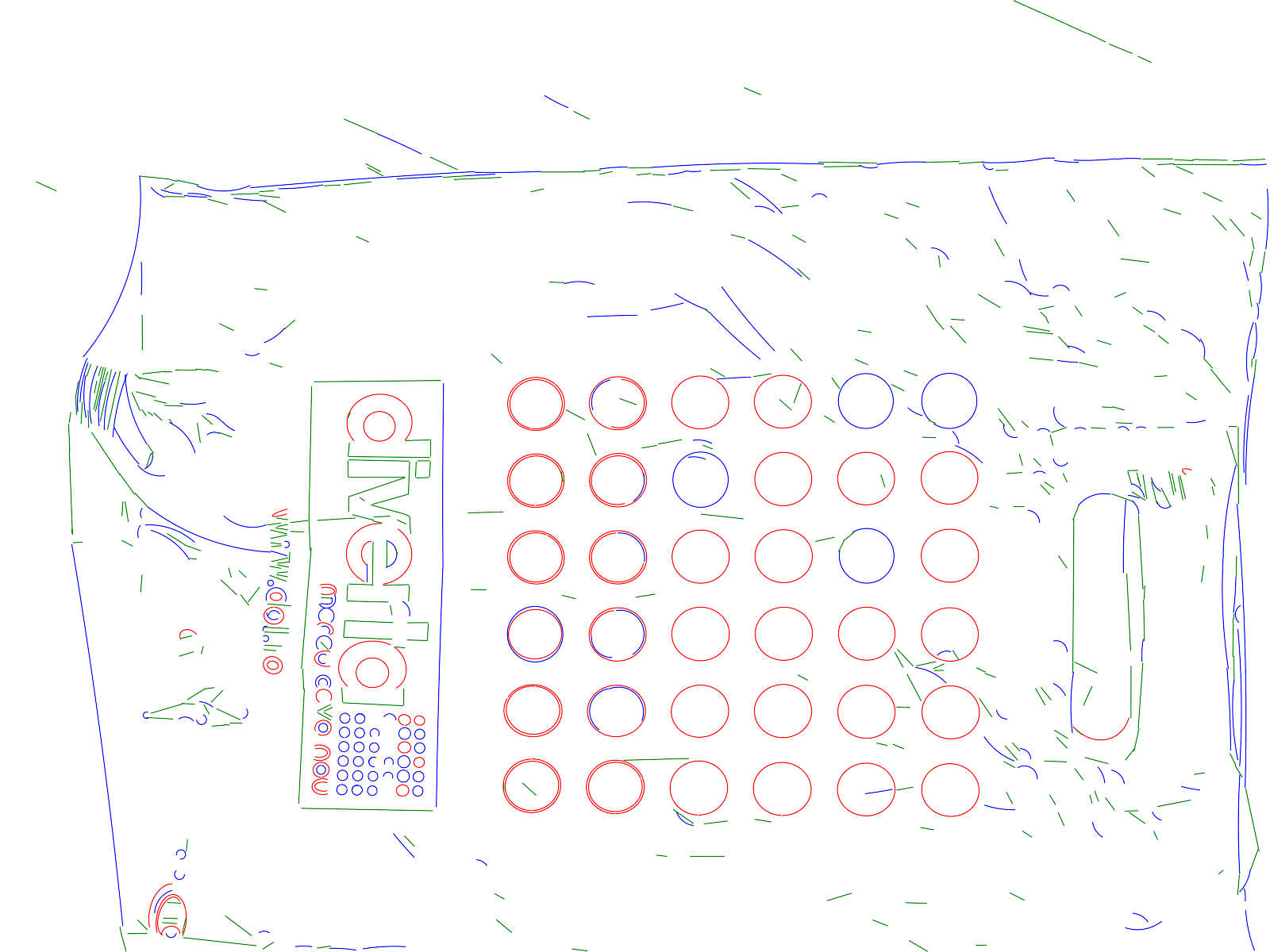
Here are some results of ELSD applied on real images. For each row: original image, ELSD result, Etemadi result [5], Hough-based circle detector result. For more examples, see the archive of the online demo (user: demo, pass: demo).

Image size: 445 x 304 pixels, ELSD execution time: 1s
Image size: 640 x 480 pixels, ELSD execution time: 0.4s
Image size: 442 x 450 pixels, ELSD execution time: 0.6s
Image size: 1600 x 1200 pixels, ELSD execution time: 1.3s
Image size: 1600 x 1200 pixels, ELSD execution time: 3.1s
Image size: 612 x 563 pixels, ELSD execution time: 0.1s

Conclusion

Efficient (multiple) geometric shape detectors can be obtained using the scheme: hypothesis selection, validation (and model selection).
Ellipse fitting: more accurate using simultaneously positional and tangential constraints.
Model selection: needs improvement to handle correctly polygonal shapes.

References

[1] Desolneux, A., Moisan, L., Morel, J.M.: From Gestalt Theory to Image Analysis: A Probabilistic Approach. Springer-Verlag (2008)
[2] Grompone von Gioi, R., Jakubowicz, J., Morel, J.M., Randall, G.: LSD: A fast line segment detector with a false detection control. PAMI 32, 722-732 (2010)
[3] Pătrăucean, V.: Detection and identification of elliptical structure arrangements in images: Theory and algorithms. PhD thesis. University of Toulouse, France, http://ethesis.inp-toulouse.fr/archive/00001847/
[4] Hartley, R.I., Zisserman, A. : Multiple View Geometry in Computer Vision, 2nd edn. Cambridge University Press (2004)
[5] Etemadi, A.: Robust segmentation of edge data. In: Int. Conf. on Image Processing and its Applications. 311-314 (1992)