ELSD (Ellipse and Line Segment Detector)
by Viorica Pătrăucean, Pierre Gurdjos,
and Rafael Grompone von Gioi
About
This is the homepage of
ELSD (Ellipse and Line Segment Detector). ELSD
is a parameterless detector, that can be applied on any grey-scale image
without prior edge detection or parameter tuning.
Example:
| Original image |
ELSD result |
 |
 |
The preprint of the article published at ECCV2012 A parameterless line segment and elliptical arc
detector with enhanced ellipse fitting. The source code of ELSD can be
found here. Note that a newer improved version of the algorithm is available here.
It might be useful to test online our detector, before downloading and
compiling it. A demo where users can upload their images and test ELSD
is available here demo (user: demo, pass: demo).
Check out the result of ELSD
applied on a real video (frame size: 638x360, average execution time
0.7s/frame).
For any questions or remarks, please contact the corresponding author at
vpatrauc at gmail dot com.
Here follows a summary description of ELSD.
Abstract
Geometric shape detection (line segment, ellipse) is often a prerequisite for
high level tasks; hence we need
automatic detectors, i.e.
no
parameter tuning.
ELSD
- parameterless Ellipse and Line Segment Detector;
- works with grey-scale images (no edge detector needed);
- grounded on the a contrario theory [1], it controls statistically
the number of false positives; extends LSD [2];
- it offers a better precision due to enhanced ellipse fitting.
ELSD Overview
We pose the geometric shape detection in the statistical framework of
multiple hypothesis testing, in order to focus on reducing/controling
false detections.
The main steps of ELSD are:
- 1. Hypothesis selection:
- - heuristic, but free of critical
parameters in order to avoid false
negatives.
- 2. Validation:
- - parameterless, grounded on a contrario theory; controls the number of false positives.
- 3. Model selection:
- - parameterless; follows Ockham’s razor principle.
1. Hypothesis Selection
This step must produce line segment and elliptical candidates.
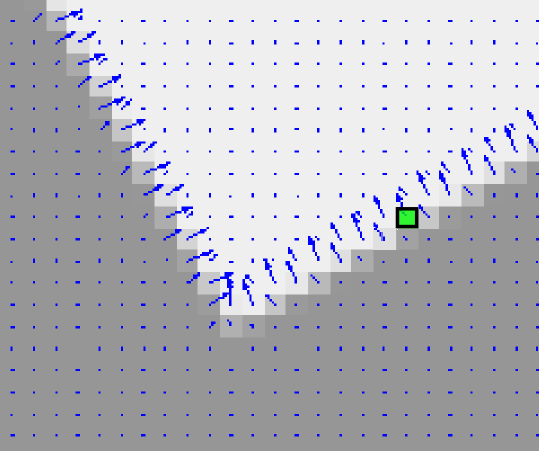
- A. Region grow
- - starting from a seed pixel, gather recursively neighbour pixels with
similar gradient orientation.
- B. Curve grow
- - gather recursively neighbour regions that follow a convex, roughly
smooth contour.
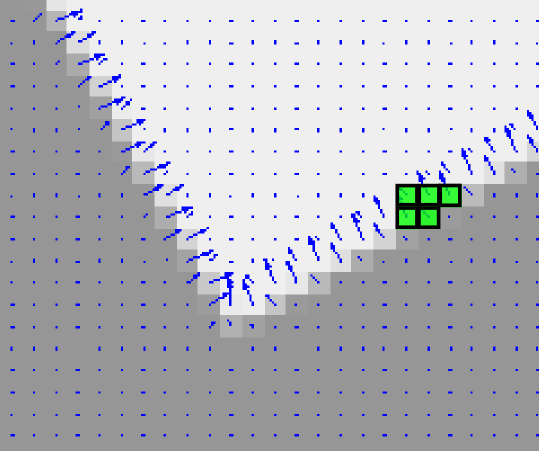
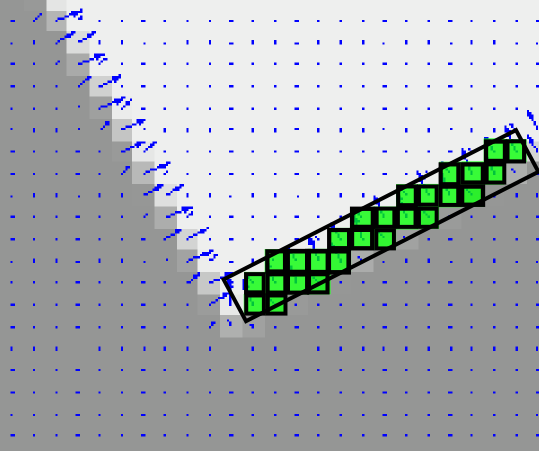
- C. Fitting:
- - pixels gathered in steps A and B respectively, are used to estimate the line segment and the elliptical hypotheses
- region => rectangle fit => line segment hypothesis;
- curve => circular/elliptical ring fit => circle/ellipse
hypothesis.

- - The tangent to the conic in a point pi is also the
polar of the point pi w.r.t. the conic [4].
- The algebraic distance error and the gradient orientation error
can be
simultaneously minimised through a non-iterative procedure. This
improves the accuracy, especially when pixels are sampled along
incomplete circles/ellipses.
2. A Contrario Validation
The
a contrario theory uses the non-accidentalness principle;
informally, it says that "we see nothing in noise". Thus, hypotheses that are
likely to be observed in noise should be automatically discarded. To this end
we need to define two elements: a model of "noise" (unstructured data) and a
function to measure the quality (degree of structuredness) of a hypothesis.
- Model of unstructured data:
- - field of gradients whose orientations can be considered i.i.d. random variables
=> Gaussian white noise image;
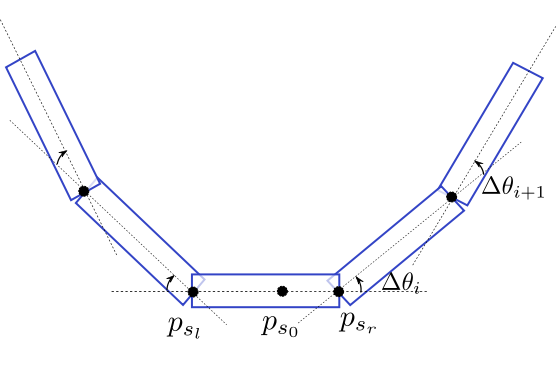
- Degree of structuredness:
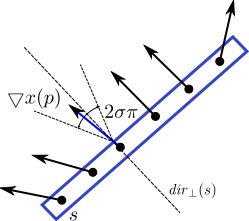
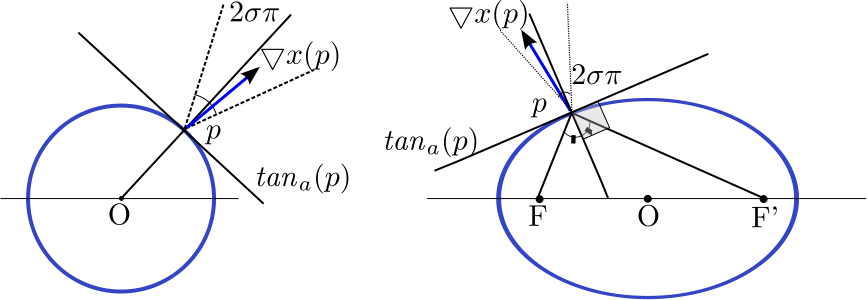
- - the number of σ-aligned pixels contained in a hypothesis. For a line segment, a pixel is said to be σ-aligned
if its gradient orientation is orthogonal to the line segment, up to a
precision σ (see left figure below). Similarly, for circle/ellipse case,
a pixel is σ-aligned if its gradient orientation is orthogonal
to the tangent to the circle/ellipse in that point (see middle and right
figures bellow).
 |
 |
- Validation test:
- - accept as meaningful hypotheses only those too
structured to
appear by chance in unstructured data. If a hypothesis contains
too many aligned points, it is not likely for it to be observed in
noise; thus it is meaningful.
The Number of False Alarms (NFA) is the essential quantity used to assess the validity of a hypothesis, and is given by:
NFA=N⋅Β(l,k,σ), where
N - number of hypotheses (n5 line segments,
n6 circular arcs, n8 elliptical arcs,
for an nxn image);
l - number of pixels in hypothesis;
k - number of aligned pixels in hypothesis;
Β(l,k,σ) - binomial tail = ∑
li=k C
li σ i(1-σ)
l-i.
A hypothesis is considered meaningful iif it satisfies the validation test NFA ≤ ε.
Control of false positives: If a hypothesis is accepted as meaningful only when the above validation test stands, then
the number of meaningful hypotheses observed by chance in unstructured data is less than ε (see the paper for a proof of this proposition).
3. Model Selection
When more than one hypothesis passes the validation test, a model
selection needs to be performed to choose the most suitable geometric
interpretation for the given data.
Ockham's razor principle recommends to
- choose the best geometric interpretation for the data,
- but penalize complexity.
We use NFA as model selection criterion [3] and keep as valid hypothesis the one with the lowest NFA.
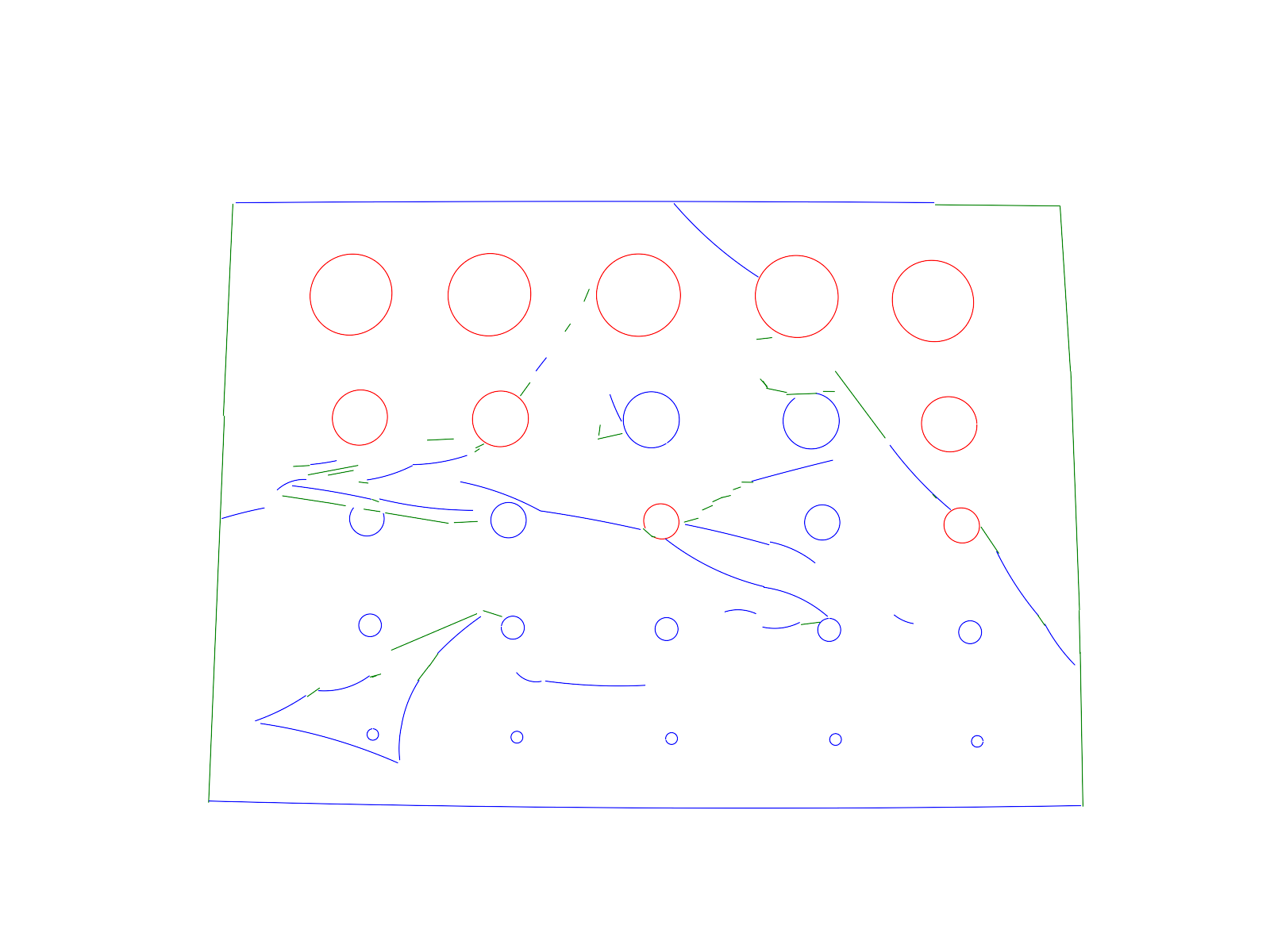
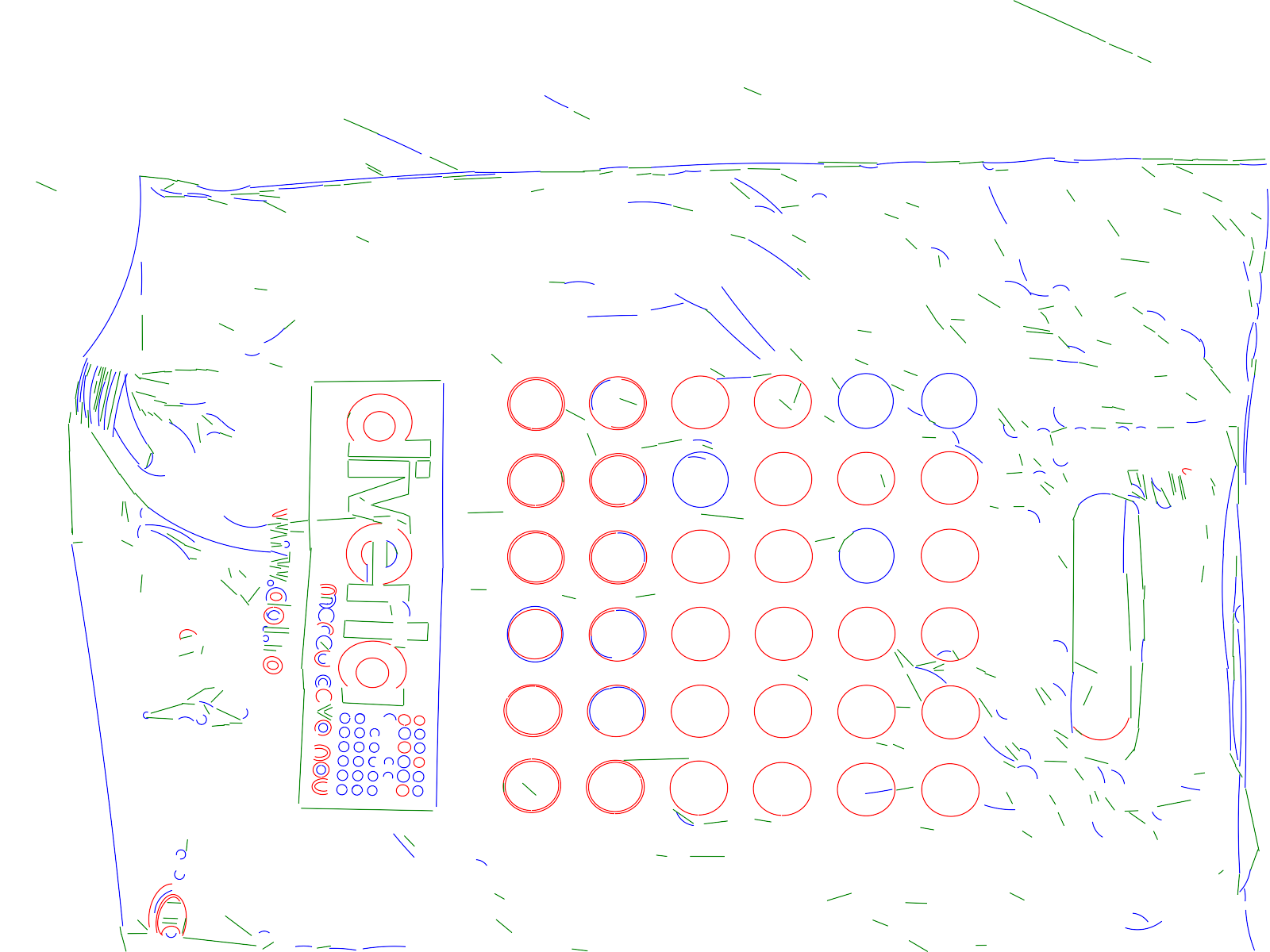
Results
Here are some results of ELSD applied on real images. For each row: original
image, ELSD result, Etemadi result [5], Hough-based circle detector result. For
more examples, see the archive of the
online demo (user: demo, pass: demo).
 |
 |
 |
 |
| Image size: 445 x 304 pixels, ELSD
execution time: 1s |
 |
 |
 |
 |
| Image size: 640 x 480 pixels, ELSD
execution time: 0.4s |
 |
 |
 |
 |
| Image size: 442 x 450 pixels, ELSD
execution time: 0.6s |
 |
 |
 |
 |
| Image size: 1600 x 1200 pixels, ELSD
execution time: 1.3s |
 |
 |
 |
 |
| Image size: 1600 x 1200 pixels, ELSD
execution time: 3.1s |
 |
 |
 |
 |
| Image size: 612 x 563 pixels, ELSD
execution time: 0.1s |
Conclusion
Efficient (multiple) geometric shape detectors can be obtained using the
scheme: hypothesis selection, validation (and model
selection).
Ellipse fitting: more accurate using simultaneously positional
and tangential constraints.
Model selection: needs improvement to handle correctly polygonal shapes.
References
[1] Desolneux, A., Moisan, L., Morel, J.M.: From Gestalt Theory to Image
Analysis: A Probabilistic Approach. Springer-Verlag (2008)
[2] Grompone von Gioi, R., Jakubowicz, J., Morel, J.M., Randall, G.: LSD: A
fast line segment detector with a false detection control. PAMI 32, 722-732
(2010)
[3] Pătrăucean, V.: Detection and identification of elliptical structure
arrangements in images: Theory and algorithms. PhD thesis. University of
Toulouse, France,
http://ethesis.inp-toulouse.fr/archive/00001847/
[4] Hartley, R.I., Zisserman, A. : Multiple View Geometry in Computer
Vision, 2nd edn. Cambridge University Press (2004)
[5] Etemadi, A.: Robust segmentation of edge data. In: Int. Conf. on Image
Processing and its Applications. 311-314 (1992)

This Website Visits